Page 70, top. Corrections in Eq. (3.64), (3.65) and related
text:
with the constraint
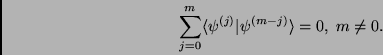 |
(3.64) |
Here are collected all terms of order
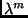 and then
and then 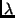 is set to
is set to  . Taking matrix
elements of
(3.63) leads to
. Taking matrix
elements of
(3.63) leads to
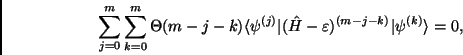 |
(3.65) |
where
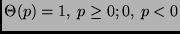 .
The desired expressions can be derived by applying the condition
that
(3.65) be variational with respect to
.
The desired expressions can be derived by applying the condition
that
(3.65) be variational with respect to 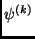 at each order
at each order
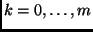 .
.
Richard Martin
2004-05-25